長山雅晴教授

NAGAYAMA Masaharu

数理科学系

所属: 電子科学研究所

研究分野: 応用数学

キーワード: 反応拡散系, 数値計算, 数理モデル

研究概要

研究内容

我々の研究目標は、数理モデル化と数値計算，数理解析を用いて、
非線形現象のメカニズムを数理的視点から理解することです。
例えば、液滴や粒子の運動、化学反応、細胞動力学の研究をしています。

主要論文

M.Nagayama, M.Yadome, N.Kato, J.Kirisaka, M.Murakami and S.Nakata, “Bifurcation of self-motion depending on the reaction order”, Physical Chemistry Chemical Physics, 11(2009) 1085-1090.
M.Nagayama, S.Nakata, Y.Doi and Y.Hayashima, ” A theoretical and experimental study on the unidirectional motion of a camphor disk “, Physica D, 194(2004) 151-165.
M.Mimura and M.Nagayama, “Nonannihilation dynamics in an exothermic reaction-diffusion system with mono-stable excitability”, CHAOS 7(4) (1997) 817-826.

研究者総覧

https://researchers.general.hokudai.ac.jp/profile/ja.e7dbe3d3415fe41d520e17560c007669.html

連絡先

nagayama（at）es.hokudai.ac.jp

学生へのひとこと

数学という学問が自然現象や生命現象の理解に役に立つ面白さを一緒に感じてみましょう！

インタビュー

①出身高校・大学を教えてください

出身高校は岡山県立倉敷天城高等学校です。大学は徳島大学に進学、修士課程で広島大学大学院理学研究科数学専攻に進学し、博士課程で東京大学大学数理科学研究科に進学しました。
指導教員の先生が広島大学から東京大学に異動された関係で、博士課程は東京大学に進学しました。

②いつごろから数学の道に進むことを決めましたか？

高校生の頃から数学の勉強するのは好きでしたけど、得意なほうじゃなかったかな（笑）
数学者になろうとは考えてなかったですけど、修士課程のときに反応拡散系の数値シミュレーションが面白くて、そのときに「こんな研究をこのまま続けていけたらいいな」という思いはありました。そのまま延長して現在に至っています．

③子供のころとかはどうでしたか？

子供のころは一人で、いろいろなことをイメージしながらオモチャで遊んでいました。勉強はほとんどしていなかったですね．現在の研究は，子供の頃にやっていたこととほとんど同じような思考で行っている気がします。
数理モデリングの研究はイメージが大事なのです。数式を作る時は現象をイメージしながら作っています。そう考えると今はおもちゃが数式になっているだけですよね。

④研究内容について教えてください。

私の研究内容は基本的に様々な現象、自然現象や生命現象を数式で表現し、数理的に理解することです。言うならば、現象を数学の言葉に焼きなおして、理論的に理解したいということです。そのために現象の数理モデリングを行っています。数理モデルを使って現象の理論的理解を進め、数理モデルから予想されることを実験にフィードバックし、新しい現象の発見につなげようとする研究を現在は行っています。
自然現象等が研究対象なので、基本的には実験系の研究者と共同研究を行っています。実験家と議論することで、「数学的にはこのように表現できますが、いいですか？」と言ったディスカッションをしつつ研究を進めています。そして幸運にも数学として取り組むことができる問題を作ることができれば、そのときは数学解析を行っています。本当は全ての数理モデルで数学解析をしたいのですが、ほとんどの問題が数学解析を行うことが困難なので、数値シミュレーションを使って数理モデルに対する数理解析を行っています。そして数理モデルから出てくる予測を実験グループにフィードバックするように努力しています。残念ながら、なかなか実験可能な予測は出てきませんがね（笑）。

⑤具体的な内容はどういうものですか？

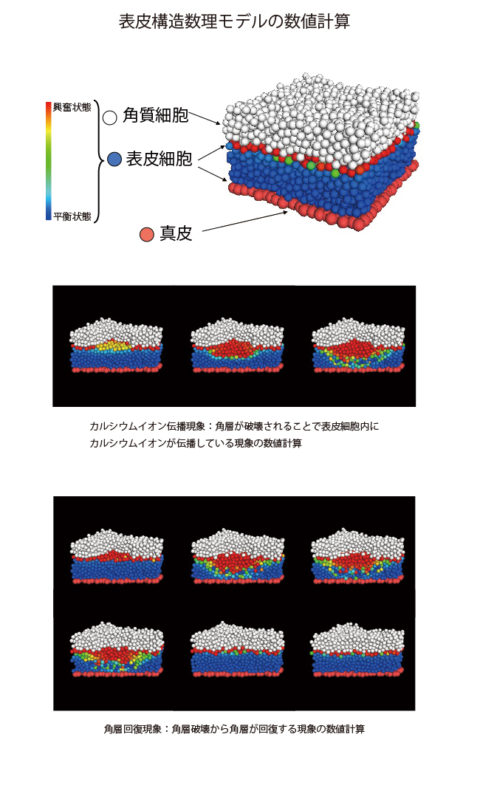
様々な現象の数理モデルを作っていますが、最近では皮膚の数理モデリングを主に研究しています。皮膚は目に見える身近なものなのですが、わからないことばっかりなのです。注目しているのは皮膚の持っているバリア機能です。皮膚の持つ重要な機能の一つで、バリア機能とは人体の保水機能と外部からの異物の侵入を防ぐ機能のことですが、これは皮膚の最も外部にある角層が担っています。私たちは、表皮細胞内のカルシウムイオンダイナミクスに注目して、バリア機能が作られる機構と維持される機構、そしてバリア機能が低下する機構を数理モデルから理解しようとする研究です。この研究をさらに進めて In Silico実験系の構築を目指しています。
非常に簡単な…簡単と言っても１０変数ぐらいある数理モデルなのですけど、この１０変数ぐらいの方程式系を相互作用させて数値シュミレーションすると、あたかも本物のような皮膚が形成されて、恒常的維持されているように見えます。その中から、なぜ皮膚がこのように自然に形成されるのか？かという問いを、数学的にこういうことが大事なのではないかとか議論しています…。なかなか難しいですけどね。数学として解くとこのできる問題が出てくるような気はまだまだしないですね。
ほかには、自己駆動系の数理モデルとその数理解析を10年位続けて研究していますね。例えば、表面張力の変化を使って動く物体や液滴を、あるいは細胞でもいいのですが、対象にして、数理モデルを作り、動くメカニズムを数理的に理解する、という研究をしています。この研究は比較的数学と相性のよい問題になっていて、数値シミュレーションだけではなく、解の存在やその線形化安定性解析、分岐解析といった数学解析も行っています。

―皮膚の方は企業の人との研究ですか？

はい，資生堂との共同研究です。

―資生堂の人っていうのはやはり研究者なのですか？

そうですね。資生堂リサーチセンターの研究員の方々ですね。

―ちなみに何か製品にはなりましたか？

私が共同研究を始めてから製品になったものはないと思っていますが…、私は何が製品になるのかはわからないです。これからそういうことができればいいですね。
肌荒れとか、アンチエイジング、かゆみのメカニズムなどを数理科学と生理学実験の融合研究によって理解(解明)しようとしているので、これらのものに関連する製品を作ることができればと考えています。資生堂は化粧品会社ですけど、最終的には医療の基礎につながればいいというイメージをもっています。
言うのは簡単なのですが、かゆみの起こる原因を考えようとしても、かゆみの定義って何？という感じでなかなか研究が進みませんね。「かゆみ」と言う感覚的なものを何かの量で定義しないと数理科学として議論をすることができないですよね。皮膚科学を数理として議論するための数理皮膚科学のような学問を無意識に作ろうとしている感じがありますね。

⑥自走する粒子も共同研究ですか？

そうですね。もともとは化学の実験系の研究者と共同研究を始めて、徐々に物理系の人たちも加わって現在の共同研究の形になりました。
数理モデルで初めて作ったのが自走粒子系でした。それまでは数理モデリングの研究はやってなくて、反応拡散系に現れるパターンダイナミクスの計算機援用解析を行っていました。もうちょっと実体のある研究がやりたなと自分の中であったので…（反応拡散系に実体がないといったら怒られますけど（笑））
当時は、そんなに実体のある反応拡散系の研究をしていなかったので、もうちょっと現象に近い研究がしたかったというのがありました。ちょうどその頃、現在の共同研究者たちと知り合いになったので、自走粒子の数理科学的研究を始めることになりました。
実は皮膚に関する共同研究者も共同研究グループの繋がりから知り合いになりました。
化学実験系の研究者が資生堂の人が共同研究していて、表皮細胞間のカルシウムイオン伝播現象について相談されて、そこから現在の共同研究が生まれました。
人と人の繋がりで共同研究が広がっていきました。

⑦印象に残った出来事は？

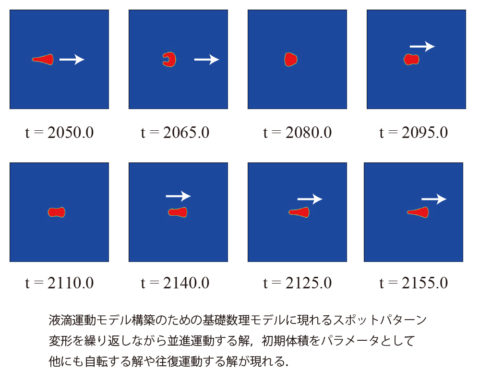
化学反応を伴う自走粒子運動の問題の中で、自走粒子から拡散する界面活性剤が中和反応によってイオン化して、振動運動をする実験系での出来事です。
反応次数によっては振動現象が起きないことを数理モデルの数値計算から予測し、実験によって実証できたことです。予測してから、実証まで７年かかりましたけどね（笑）。
その実験系はリン酸水溶液上を樟脳酸船が振動する実験系でした。実験系を再現できる数理モデルを使って、反応次数を変更すると、ある反応次数では振動が起きなくなったのです。「反応次数が２の系では起きませんよ！」ってことです。
一般的には、理論で示唆した反応次数の実験系を見つけることは難しいのですが，たまたま見つけることができ、1年間検証した結果、振動しないことがわかりました．共同研究者の学生の卒業研究で検証したのですが、振動するかどうか、やってごらんと渡したら１年間振動しなかったということです（笑）反応次数に依存して振動しないことが本当にあるのだと…実験では、都合よく振動する反応系を選ぶことができましたよね。

⑧大学院生でもそういう研究に携わっている人はいますか？

皮膚の数理モデルの研究については２人の学生が研究をしています。この問題は結構難しくて、修了できないと困るので、あんまりやらせたくないですね（笑）
自己駆動粒子運動の数理解析を行っている学生も２人、あとはMDCK細胞の運動に対する数理モデルの研究をしている学生もいます。
最近生命系の研究者たちと共同研究を始めたので、細胞運動とか神経細胞分化の問題を大学院生と一緒に考えてみようかと思っています。

⑨就職はどんなところにしてますか？

北海道に来てまだ１年で、北海道大学ではまだ卒業生が出ていないので就職先はわかりません。前任の大学では、大学院に進学する学生が多く、修士課程修了後は大手に就職した学生が多いです。
例えば、東芝、富士通、オムロン、日鉄日立ソフトウエア、アイシン・エイ・ダブリュ等です。また、博士課程を修了した人は現在、博士研究員として大学等で研究を行っています。

⑩修士の学生で受け入れるとしたらどんな人に来て欲しいですか？

線形代数と微分積分学は最低ちゃんと勉強している人に来て欲しいです。あとは、興味のあることを頑頑張って続けることができる人ですね．基本的に付きっ切りで指導しないので、こんな研究やったらおもしろいかなと思えることを、自ら進んで勉強してくれる人ですね。わからないことがあった当然一緒に議論しますが、とにかく自分で考えようとする人に来て欲しいですね。線形代数と微分積分ができれば、あとは必要なことがあれば、必要になったときに勉強したらいいじゃない、といつも言っています。
数値計算はうちの研究室秘伝の入門書があるので、それを使って勉強すればある程度まではできるようになります。
コンピュータを触るのが嫌い、という人だとちょっと困りますが、「触ることには抵抗ないけども、プログラミングはそんなにできません。」という学生でも問題ないです。徐々にできるようになります。
修士から研究室に配属された学生には、最初の２ヶ月ぐらいは数値シミュレーション入門を集中して勉強してもらい，平行してセミナーの勉強をしてもらいます。４年生から研究室に配属された学生は、セミナーと同時進行しながら数値シミュレーションを４ヶ月位で終わるようにがんばってもらいます。
大変ですが、そういうことを経験してきた先輩たちが教えてくれるので大丈夫です。

⑪高校生または大学生にアドバイスはありますか？

普段から、みんなが当たり前って思えることに疑問を持って「なぜか？」と考えられるようになって欲しいですね。そして、「これはなぜ？」って自然に考えられるような人はぜひ、理学系に進学して欲しいですね。普通のことがなぜと思える人。そういう人にはお勧めします。ぜひ来てください。研究室でお待ちしております。

2013年(平成25年) 6月インタビュー実施