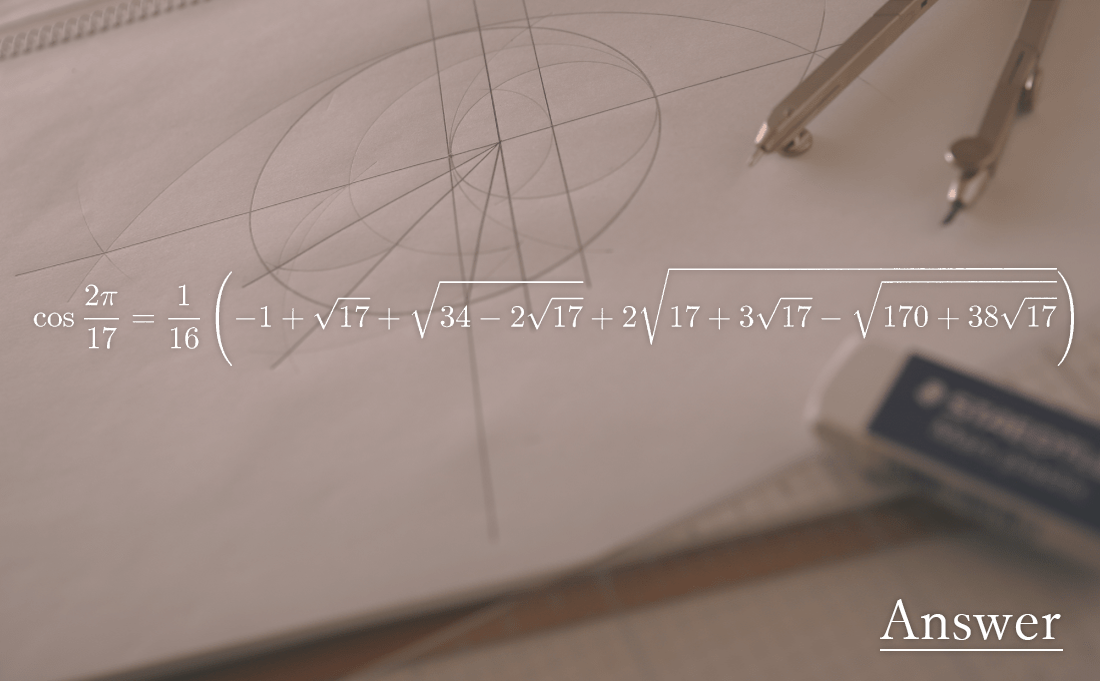数学に関するエピソード（5）

高校で習う三角関数サイン、コサイン、ところでcos(2π/17)がこんな値だったって知ってました？実は、この公式、ある事実と関係しているのですが、それは何だと思いますか？

実は、正17角形が定規とコンパスで作図可能であることをこの公式は表しています。
ポイントはルート \(\sqrt{}\) だけ使って表せている点です。これはガウスによって発見されました。
彼はさらに \(2^{2^n}+1\) という形をした素数pに対して \(\cos \frac{2\pi}{p}\) がやはりルートだけを使って
表されることを示しました。これは現代数学におけるガロア理論の先駆けとなった研究です。
北大数学科では、ガロア理論を学部3,4年の講義で学びます。

また正ｎ角形の頂点を複素平面の点で表すと \(e^{\frac{2\pi i}{n}}\)ですが、これは円分数と呼ばれ、円分数に関する整数論＝円分体論は現代でも活発に研究されている分野のひとつです。
そしてこの理論の延長線上には、フェルマー最終定理の解決という偉業がありました。
正多角形の作図問題が、ガロア理論や円分体論、そしてフェルマー最終定理といった拡がりをもっているなんて驚きですね！