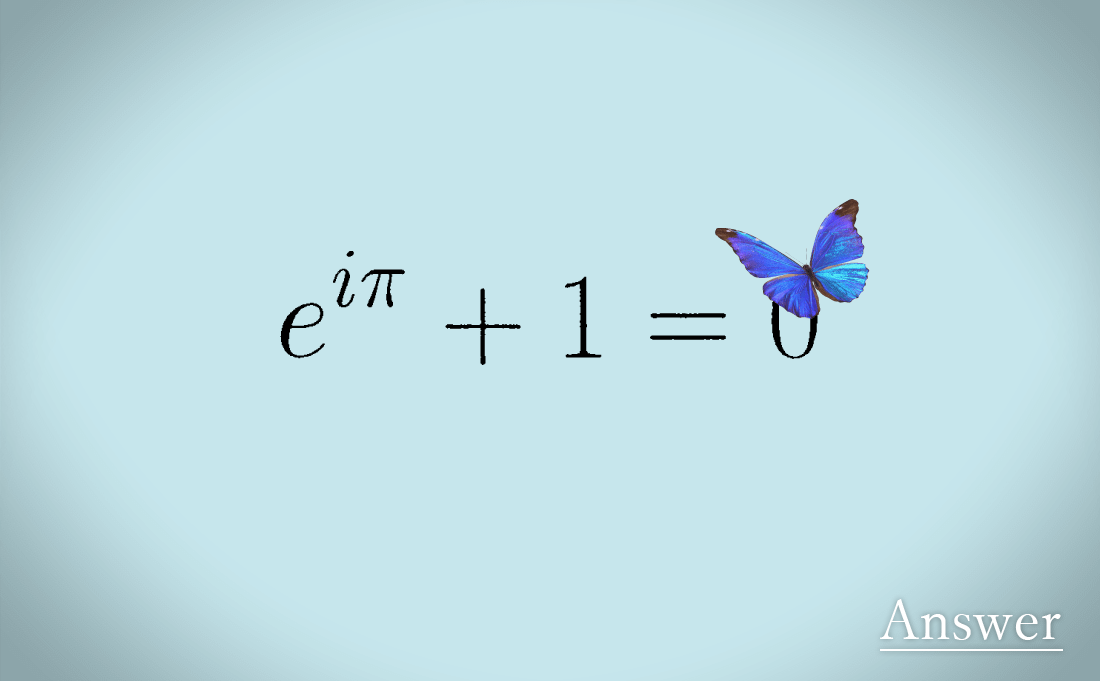数学に関するエピソード（1）

科学における最も重要な定数「1, 0, π, e, i」と演算「和・積・冪」を驚くべき簡潔さで関係付けるオイラーの恒等式とは

オイラーは著書“Introductio in analysin infinitorum”（1748）において、三角関数や指数関数、対数関数など、多様な個性を持つ対象を無限級数、超越関数という観点で統一的に扱い、それらが織りなす調和の世界 – 数学における最も美しい式と称される「オイラーの恒等式」を含む – を明らかにしました。本著はそれまでの数学の景色を一変させたと言われています。多様な個性のなかに潜む統一性を見出す視点、新たな観点を提示して、その遥か先に進むオイラーの手法は現代数学の研究の王道の一つでもあります。
北大数学では無限級数やテイラー展開を含む解析学の基礎、複素関数論を学部2・3年生で学びます。