| 研究テーマ | 群論、スピン波理論、ランチョス厳密対角化法などの解析的・数値的手法に基づく準結晶中の電子・スピンの振る舞いの解明。準周期性がもたらす新奇物性探索と、準周期系に適用可能な新規計算手法開発。 |
| 研究分野 | 物性理論, 強相関電子系, 計算物理学 |
| キーワード | 準結晶, 磁性, 群論, スピン波理論, ラマン散乱, 動的構造因子, グリーン関数, 配位間相互作用, 補空間, 閉じ込め状態 |
研究紹介
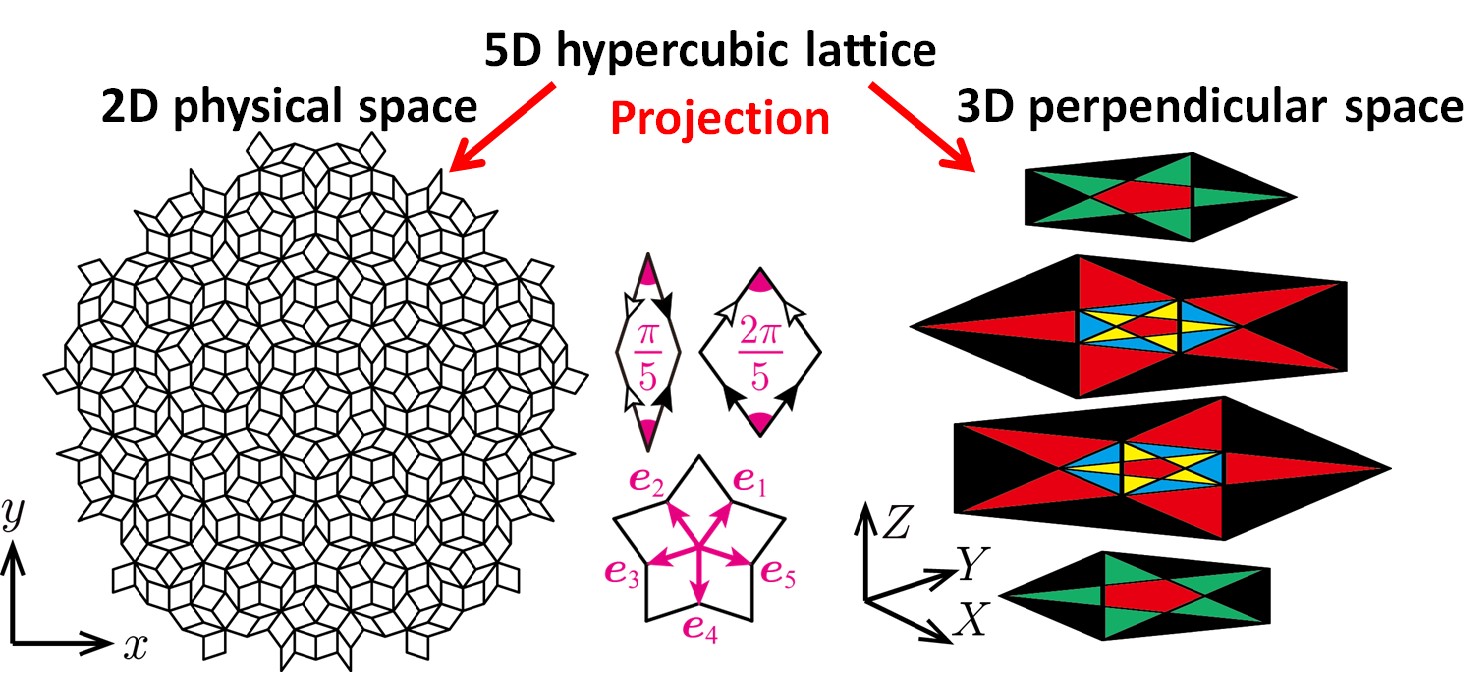
従来の結晶は、単位構造が規則正しく繰り返される「周期性」を持つのが特徴です。これに対し準結晶は「準周期性」という新たな秩序を持ちます。準結晶の構造は、5回、8回、10回、12回といった高い回転対称性を示しますが、これは周期性を持つ結晶では許されない対称性です。また、準結晶は黄金比のような無理数や、フラクタル(自己相似性)とも深く関係しています。さらに、準結晶は高次元の周期結晶を2次元や3次元空間に射影した断面構造として理解され、「補空間」と呼ばれる実空間と直交した余剰空間を持ちます。私はこのような準結晶の高次元性や高対称性が、電子状態やスピン自由度の物性にどのように影響するのかを、理論面から解明することを目指しています。また、準結晶に限らず、電子系・スピン系の多様な物性をより良く記述するための、新たな数値的・解析的手法の開発にも興味を持って研究しています。
| 学位 | 博士(理学) |
| 自己紹介 | 北海道出身です。物性理論や計算物理、特に強相関電子系を中心に研究してきました。最近はなかなか行けていませんが、パークゴルフが好きです。 |
| 所属学会 | 日本物理学会 |
| 居室 | 理学部2号館 2-11-16号室 |