INOUE Takashi
Assistant Professor
Shedding Light on the “Third Solid”: Quasicrystals
Department of Physics, Condensed Matter Physics

| Theme | Elucidating the behavior of electrons and spins in quasicrystals using analytical and numerical approaches, such as group theory, spin-wave theory, and the Lanczos exact diagonalization method. Exploring novel physical properties emerging from quasiperiodicity and developing new computational techniques applicable to quasiperiodic systems. |
| Field | Condensed Matter Theory, Strongly Correlated Electron Systems, Computational Physics |
| Keyword | quasicrystal, magnetism, group theory, spin-wave theory, Raman scattering, dynamic structure factor, Green's function, configuration interaction, perpendicular space, confined state |
Introduction of Research
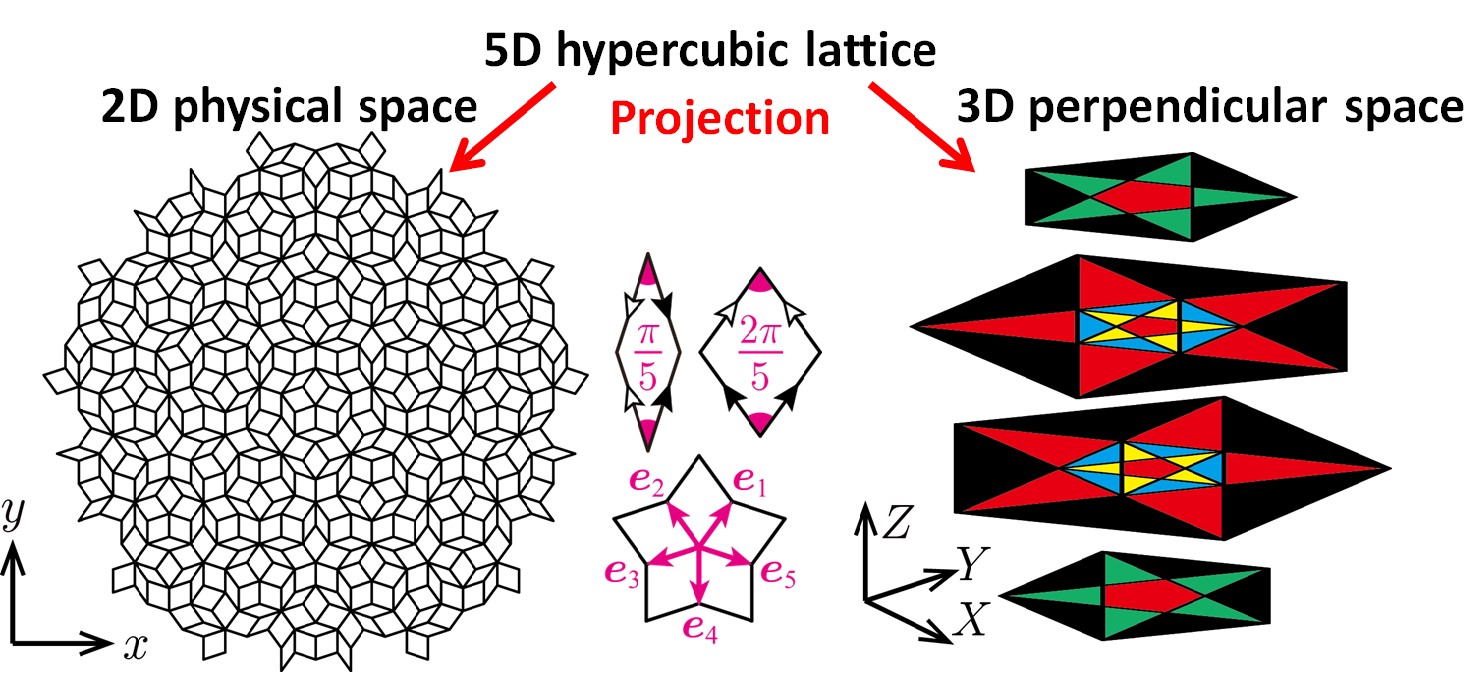
Conventional crystals are characterized by “periodicity”, where unit structures repeat regularly in space. In contrast, quasicrystals have a new type of order known as “quasiperiodicity”. Quasicrystal structures exhibit high rotational symmetries, such as 5-, 8-, 10-, and 12-fold symmetry, which are forbidden in periodic crystals. Quasicrystals are also deeply connected to irrational numbers like the golden ratio and to fractals (self-similarity). Furthermore, quasicrystals can be understood as projections of higher-dimensional periodic crystals onto two- or three-dimensional space. In this framework, they possess a so-called “perpendicular space”, an additional dimension orthogonal to real space. My research aims to theoretically explore how such high dimensionality and high symmetry in quasicrystals manifest in electronic states and spin degrees of freedom. I am also interested in developing novel numerical and analytical methods to better describe a wide range of physical properties in electronic and spin systems, not limited to quasicrystals.
| Academic degree | Ph. D. |
| Self Introduction | I’m from Hokkaido. My research has focused on condensed matter theory and computational physics, particularly strongly correlated electron systems. I haven’t had much time recently, but I enjoy playing park golf. |
| Affiliated academic society | The Physical Society of Japan |
| Room address | Science Building 2 Room 2-11-16 |