数値近似解法のひとつの理論的裏付けに世界で初めて成功
【ポイント】
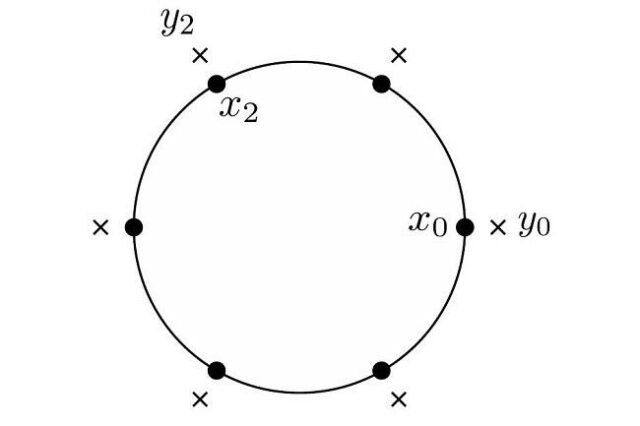
- 修正ヘルムホルツ方程式(※1)という方程式の円領域上の場合について、基本解近似解法(※2)による近似解(※3)の存在と、真の解への指数的収束(※4)を示しました。
- 今回の修正ヘルムホルツ方程式はノイマン型の境界条件(※5)が課されており、この問題に対する基本解近似解法の解の構成と、特に指数収束の数学的結果は世界初の結果です。
- この結果から、修正ヘルムホルツ方程式のノイマン問題に対する一般領域の場合における基本解近似解法の理論的裏付けが可能になることができると期待できます。また反応拡散系の一般領域に対する進行スポット解の運動の解析にも応用することができます。
【概要】
北海道大学の栄 伸一郎教授(理学研究院 数学部門)、公立はこだて未来大学の田中吉太郎准教授、九州大学の落合啓之教授の共同研究グループは、数値解析分野における一つの数値解法の理論的な裏付けをするのに成功しました。
本グループは、円領域上の修正ヘルムホルツ方程式の近似解を基本解近似解法という方法を用いて構成し、真の解に指数的に収束することを示しました。今回の修正ヘルムホルツ方程式はノイマン型の境界条件が課されており、この問題に対する基本解近似解法の解の構成と、特に指数収束の数学的結果は世界初です。
(背景)
反応拡散系と呼ばれるある方程式の解の中には、形を一定に保ったまま伝搬できる進行スポット解と呼ばれる解があります。この解の運動が、領域の形状にどのような影響を受けるのかという問題は細胞生物学や非平衡化学の分野で興味をもたれている重要な研究課題です。 北海道大学の栄伸一郎教授は、領域内部のスポット解の運動と領域の形状の関係を、運動方程式の形で導出することにより明らかにしました。しかし、この運動方程式を解くためには、修正ヘルムホルツ方程式と呼ばれる方程式の解が必要であり、この解の存在自体はわかっていたものの、特定の領域を除いて、この解の表示式は求められていませんでした。この問題がJST未解決問題ワークショップに出題され、これがきっかけで共同研究が始まりました。(関連HP:JST 数学領域 未解決問題ワークショップ )
研究成果の詳細および※用語説明はプレスリリースをご覧ください。






